Friday, May 22, 2015
Friday, May 1, 2015
Reading tables/graphs
In this lesson we will learn what to do with a table or a bar graph which contains mathematical data.
THE PURPOSE of a table or a graph is to ORGANIZE data to allow an ANALYSIS of the data to enable the mathematician to make good DECISIONS based upon COLLECTED data.
An example of a table that you are already using but probably did not even know about - is located in your cell phone. Your phone contains phone numbers of everyone that you know.
If these numbers were recorded on paper, they would be written down beside a name to identify who the number belonged to just like "the table" that you see below.
This is an extremely simple table, whose PURPOSE is to organize a series of phone numbers into a list that correctly associates a unique number to a specific name.
Now what I have done for you is to combine a BAR GRAPH and a TABLE to show how the data (information) that each one of these graphs/tables contain can be ORGANIZED and ANALYZED to determine (in this example) who owns the most pets.
Do you recognize that . . .
1) the numbers 7, 2, 1 and 4 are all WHOLE NUMBERS.
2) each number shown is a DIGIT.
3) the PLACE VALUE of each DIGIT is positioned in the ONES PLACE.
How many pets does Jane own? The bar graph indicates "4". The table also indicates that she owns "4" pets.
Notice how the length of the BAR on the GRAPH corresponds to the number below her name in the TABLE.
Both the BAR GRAPH and the TABLE tell us the same thing - and even though each one says the same thing - they ORGANIZE the data differently.
I want to throw one more concept into the lesson at this point CHARTS.
What does a glass of lemon aid, a glass of water and a soft drink all have in common?
They all taste different but all three will quench our thirst.
A TABLE, A BAR GRAPH and A CHART all do the same thing, they just "taste" different.
The PURPOSE of TABLE, a BAR GRAPH and a CHART is to ORGANIZE data (numbers) to allow someone to ANALYZE them.
So you might be wondering "What is so important about ANALYZING data?" You need to PRETEND here for just a moment. I know with all of the electronic "things" that we use now-a-days that the IMAGINATION is not needed very often . . . BUT try to find yours and SUPPOSE that you have pet allergies really really bad. (which means that you are allergic to animal dander)
In case you don't know what DANDER is - it is skin cells similar to dandruff and some of us humans are sensitive to pet dander.
Well in our PRETEND problem - we are considering purchasing a house on Elm Street. We are bad allergic to pet dander, so it is really important to us, to know how many pets are living on Elm Street before we buy a house and move there ourselves.
The TABLE organized the data showing us the number of pets per neighbor, the BAR GRAPH organizes the information a little differently - we can tell at a glance who has the most pets (the long bar gets the prize). The CHART does exactly the same thing as the TABLE and BAR GRAPH - it is just a matter of preference.
Before we leave this lesson - I think it is important for us not to look at a TABLE, GRAPH or CHART that has already been completed for us, but that we create one of these ourselves.
Suppose you are given the following information and your goal (job) is to organize all of the data in the following paragraph so that it can be analyzed easily (at a glance).
Billy Bob is a cattle rancher who lives in Texas. Sally Sue is a doctor who lives in Alabama. Mary Jane is a teacher who lives in Oklahoma. Billy Bob lives with a wife and five children, Sally Sue lives with a husband and three children and Mary Jane lives with a husband and four children.
How would we ORGANIZE the data given to us in this paragraph so that we could tell "at a glance" which of the three states mentioned has the largest family living in it?
Step #1 -- create a table so you can ORGANIZE all of the information.
This TABLE does contain all of the necessary information BUT it is difficult to determine the answer to the question "at a glance"; therefore we will take step #2 and REORGANIZE the data above into a form that is easier to ANALYZE.
It should obvious to us now "at a glance" which state has the largest family living in it. All three methods organize the data, but each one organizes it just a little bit differently than the others. Some of prefer lemon aid, some prefer water and others prefer a soft drink . . . which one is really better - you decide . . . they all serve the same purpose.
THE PURPOSE of a table or a graph is to ORGANIZE data to allow an ANALYSIS of the data to enable the mathematician to make good DECISIONS based upon COLLECTED data.
An example of a table that you are already using but probably did not even know about - is located in your cell phone. Your phone contains phone numbers of everyone that you know.
If these numbers were recorded on paper, they would be written down beside a name to identify who the number belonged to just like "the table" that you see below.
Fred
|
479-555-1212
|
Tom
|
897-555-4789
|
Sally
|
149-555-5789
|
Jane
|
532-555-4782
|
This is an extremely simple table, whose PURPOSE is to organize a series of phone numbers into a list that correctly associates a unique number to a specific name.
Now what I have done for you is to combine a BAR GRAPH and a TABLE to show how the data (information) that each one of these graphs/tables contain can be ORGANIZED and ANALYZED to determine (in this example) who owns the most pets.
1) the numbers 7, 2, 1 and 4 are all WHOLE NUMBERS.
2) each number shown is a DIGIT.
3) the PLACE VALUE of each DIGIT is positioned in the ONES PLACE.
How many pets does Jane own? The bar graph indicates "4". The table also indicates that she owns "4" pets.
Notice how the length of the BAR on the GRAPH corresponds to the number below her name in the TABLE.
Both the BAR GRAPH and the TABLE tell us the same thing - and even though each one says the same thing - they ORGANIZE the data differently.
I want to throw one more concept into the lesson at this point CHARTS.
What does a glass of lemon aid, a glass of water and a soft drink all have in common?
They all taste different but all three will quench our thirst.
A TABLE, A BAR GRAPH and A CHART all do the same thing, they just "taste" different.
The PURPOSE of TABLE, a BAR GRAPH and a CHART is to ORGANIZE data (numbers) to allow someone to ANALYZE them.
So you might be wondering "What is so important about ANALYZING data?" You need to PRETEND here for just a moment. I know with all of the electronic "things" that we use now-a-days that the IMAGINATION is not needed very often . . . BUT try to find yours and SUPPOSE that you have pet allergies really really bad. (which means that you are allergic to animal dander)
In case you don't know what DANDER is - it is skin cells similar to dandruff and some of us humans are sensitive to pet dander.
Well in our PRETEND problem - we are considering purchasing a house on Elm Street. We are bad allergic to pet dander, so it is really important to us, to know how many pets are living on Elm Street before we buy a house and move there ourselves.
The TABLE organized the data showing us the number of pets per neighbor, the BAR GRAPH organizes the information a little differently - we can tell at a glance who has the most pets (the long bar gets the prize). The CHART does exactly the same thing as the TABLE and BAR GRAPH - it is just a matter of preference.
Before we leave this lesson - I think it is important for us not to look at a TABLE, GRAPH or CHART that has already been completed for us, but that we create one of these ourselves.
Suppose you are given the following information and your goal (job) is to organize all of the data in the following paragraph so that it can be analyzed easily (at a glance).
Billy Bob is a cattle rancher who lives in Texas. Sally Sue is a doctor who lives in Alabama. Mary Jane is a teacher who lives in Oklahoma. Billy Bob lives with a wife and five children, Sally Sue lives with a husband and three children and Mary Jane lives with a husband and four children.
How would we ORGANIZE the data given to us in this paragraph so that we could tell "at a glance" which of the three states mentioned has the largest family living in it?
Step #1 -- create a table so you can ORGANIZE all of the information.
Texas
|
Billy Bob + Wife + five children
|
Oklahoma
|
Sally Sue + Husband + three children
|
Alabama
|
Mary Jane + Husband + four children
|
This TABLE does contain all of the necessary information BUT it is difficult to determine the answer to the question "at a glance"; therefore we will take step #2 and REORGANIZE the data above into a form that is easier to ANALYZE.
It should obvious to us now "at a glance" which state has the largest family living in it. All three methods organize the data, but each one organizes it just a little bit differently than the others. Some of prefer lemon aid, some prefer water and others prefer a soft drink . . . which one is really better - you decide . . . they all serve the same purpose.
Thursday, April 30, 2015
Perimeter of a polygon
Perimeter of Polygons: Before we address this topic we need to define the two terms Perimeter and Polygon: The perimeter is the distance around the outside edge of a shape. A polygon is simply a shape as described below.
A POLYGON is a closed TWO DIMENSIONAL figure bounded by three OR MORE line segments.
You will notice that the BLUE figures are all polygons. They are flat (two dimensional figures) that are CLOSED (the black line segments completely enclose the blue interior).
There are THREE things that prevent the PINK figures from being considered POLYGONS
1) they are not flat (they are three dimensional)
2) they are made up of CURVED segments
3) they are not completely enclosed.
There are TWO different kinds or types of polygons - they are named REGULAR POLYGONS and IRREGULAR POLYGONS . . .
As you can see by these two illustrations . . . the regular POLYGONS are what we refer to as STANDARD shapes, while the irregular polygon is a NOT NORMAL shapel
So any flat (two dimensional shape) that has NO CURVES - and is completely enclosed by at least THREE line segments is a POLYGON.
Now that we have defined a POLYGON - lets take a closer look at what is meant by a perimeter.
I chose to illustrate the concept of PERIMETER by using an image of a fence. A fence like the one shown to the left is often used enclose a yard.
In the other figure below - the entire "perimeter" of the property is shown by the fence that goes ALL THE WAY around the buildings (OK use your imagination) and pretend there is "a gate" to close the gap that you see making this figure an IRREGULAR POLYGON.
So have you been able to guess what a lesson on finding the perimeter of a polygon is going to be about?
If you were the owner of a fence building company, this lesson would be VERY important to you. Your income would depend on how many feet of fence you were able to build for your customers.
OK here comes the boring technical stuff - but this stuff is what those who buy or sell fencing supplies to fence their property - use everyday . . .
A discussion about perimeters and polygons cannot begin without starting with the word GEOMETRY . . . is a word which refers to the use of math to analyze the properties of lines, angles and shapes. This is not a textbook definition, but it will do for now.
In GEOMETRY we use the mathematical property of ADDITION to find or to calculate the perimeter of a polygon (how many feet of fencing material is required to enclose a yard/field).
Technically speaking the perimeter is the distance around the outer edge of the polygon. This means that the perimeter of a polygon is the SUM of the lengths of its sides
In order to solve this problem all we need to do is to add up the lengths of all the sides.
2 in + 3 in + 1 in + 3 in + 4 in = 13 in
If we were to use our imaginations again and pretend that these units were given to us in feet as opposed to inches, we could determine how much fencing material would be required to enclose a yard with these dimensions.
Suppose you own a fence building company "Fred's Fencing". Your rent is due at the end of the month and you have an opportunity to build this fence and earn enough to pay your rent.
If your rent is $750 a month and if fencing materials cost $10 per foot, what is the total dollar amount will you need to charge to make enough money on this job to pay this months rent?
First of all you will need to FIND THE PERIMETER of this POLYGON (yard).
Add the sum of the line segments shown - 2 feet + 3 feet + 1 foot + 3 feet + 4 feet = 13 feet.
In the first place this would obviously not be a big enough yard to make very much money, especially not the $750 that we need to pay our rent. But for the sake of illustration let's continue . . .
Our fence is only 13 feet long: If our supplies cost $10 per foot, our total cost for materials will be $10 x 13 feet = $130. If we need to CLEAR $750 above the cost of material, we will need to charge the customer the following" $130 material cost + $750 labor = $ 880 for a thirteen foot section of a privacy fence.
Do you think this price is reasonable?
Just to be on the safe side - let's review addition the OLD FASHION way before calculators. I KNOW that you have a calculator and that is a good thing, BUT it is really a good thing in mathematics when the "mathematician" (that is you) is smarter than the tools they use.
We have already used the term SUM. So by now we should realize that a long time ago someone was not satisfied that there was already a perfectly good word called ADDITION. This old word means just exactly what the new word SUM means and that is "adding numbers together" to get a bigger number than we started with.
Why invent new words that mean the same thing as old words . . . I can remember when there were only a few flavors of soft drinks that had been invented and diet sodas did not even exist . . . All soft drinks quench our thirst - so why are there so many that do exactly the same thing?
If you prefer to use the word ADDITION that is OK . . . or if you choose to use the work SUM that will be OK too, because they both do and mean the same thing. Do you prefer Coke, Sprite or Dr Pepper?
In previous lessons we discussed the terms DIGITS, WHOLE NUMBERS and PLACE VALUES . . . In this lesson we have added PERIMETER and POLYGON.
Notice the extra words that have been added to our vocabulary - "addend" why don't we use digit or whole number?
Why do we prefer Pepsi over a Coke? Study the illustration given above and notice how the PLACE VALUES are still present. BEFORE calculators numbers were added together in columns just like the one shown.
The big problem in the OLDEN days was teaching the students to LINE THE NUMBERS properly when they added them together (or if you prefer calculated their SUM).
The PLACE VALUE thing has never gone away and it is important for you to realize that even with a calculator - you are adding (taking the SUM) of each PLACE VALUE. All of the ONES are added together, then all of the TENS are added together, then the HUNDREDS and so on . .
I don't mean to insult your intelligence - but you really need to be sure that you are careful when drinking your Dr. Pepper or Tab so that you do not MIX UP the place value positions when you add (calculate a SUM) to determine a total value. Just like Coke and Root Beer do not mix well together, mixing place values will give you something entirely different than what you were expecting.
F
You will notice that the BLUE figures are all polygons. They are flat (two dimensional figures) that are CLOSED (the black line segments completely enclose the blue interior).
There are THREE things that prevent the PINK figures from being considered POLYGONS
1) they are not flat (they are three dimensional)
2) they are made up of CURVED segments
3) they are not completely enclosed.
There are TWO different kinds or types of polygons - they are named REGULAR POLYGONS and IRREGULAR POLYGONS . . .As you can see by these two illustrations . . . the regular POLYGONS are what we refer to as STANDARD shapes, while the irregular polygon is a NOT NORMAL shapel
So any flat (two dimensional shape) that has NO CURVES - and is completely enclosed by at least THREE line segments is a POLYGON.
Now that we have defined a POLYGON - lets take a closer look at what is meant by a perimeter.
In the other figure below - the entire "perimeter" of the property is shown by the fence that goes ALL THE WAY around the buildings (OK use your imagination) and pretend there is "a gate" to close the gap that you see making this figure an IRREGULAR POLYGON.
So have you been able to guess what a lesson on finding the perimeter of a polygon is going to be about?
If you were the owner of a fence building company, this lesson would be VERY important to you. Your income would depend on how many feet of fence you were able to build for your customers.
OK here comes the boring technical stuff - but this stuff is what those who buy or sell fencing supplies to fence their property - use everyday . . .
A discussion about perimeters and polygons cannot begin without starting with the word GEOMETRY . . . is a word which refers to the use of math to analyze the properties of lines, angles and shapes. This is not a textbook definition, but it will do for now.
In GEOMETRY we use the mathematical property of ADDITION to find or to calculate the perimeter of a polygon (how many feet of fencing material is required to enclose a yard/field).
Technically speaking the perimeter is the distance around the outer edge of the polygon. This means that the perimeter of a polygon is the SUM of the lengths of its sides
2 in + 3 in + 1 in + 3 in + 4 in = 13 in
If we were to use our imaginations again and pretend that these units were given to us in feet as opposed to inches, we could determine how much fencing material would be required to enclose a yard with these dimensions.
Suppose you own a fence building company "Fred's Fencing". Your rent is due at the end of the month and you have an opportunity to build this fence and earn enough to pay your rent.
If your rent is $750 a month and if fencing materials cost $10 per foot, what is the total dollar amount will you need to charge to make enough money on this job to pay this months rent?
First of all you will need to FIND THE PERIMETER of this POLYGON (yard).
Add the sum of the line segments shown - 2 feet + 3 feet + 1 foot + 3 feet + 4 feet = 13 feet.
In the first place this would obviously not be a big enough yard to make very much money, especially not the $750 that we need to pay our rent. But for the sake of illustration let's continue . . .
Our fence is only 13 feet long: If our supplies cost $10 per foot, our total cost for materials will be $10 x 13 feet = $130. If we need to CLEAR $750 above the cost of material, we will need to charge the customer the following" $130 material cost + $750 labor = $ 880 for a thirteen foot section of a privacy fence.
Do you think this price is reasonable?
Just to be on the safe side - let's review addition the OLD FASHION way before calculators. I KNOW that you have a calculator and that is a good thing, BUT it is really a good thing in mathematics when the "mathematician" (that is you) is smarter than the tools they use.
We have already used the term SUM. So by now we should realize that a long time ago someone was not satisfied that there was already a perfectly good word called ADDITION. This old word means just exactly what the new word SUM means and that is "adding numbers together" to get a bigger number than we started with.
Why invent new words that mean the same thing as old words . . . I can remember when there were only a few flavors of soft drinks that had been invented and diet sodas did not even exist . . . All soft drinks quench our thirst - so why are there so many that do exactly the same thing?
If you prefer to use the word ADDITION that is OK . . . or if you choose to use the work SUM that will be OK too, because they both do and mean the same thing. Do you prefer Coke, Sprite or Dr Pepper?
In previous lessons we discussed the terms DIGITS, WHOLE NUMBERS and PLACE VALUES . . . In this lesson we have added PERIMETER and POLYGON.
Notice the extra words that have been added to our vocabulary - "addend" why don't we use digit or whole number?
Why do we prefer Pepsi over a Coke? Study the illustration given above and notice how the PLACE VALUES are still present. BEFORE calculators numbers were added together in columns just like the one shown.
The big problem in the OLDEN days was teaching the students to LINE THE NUMBERS properly when they added them together (or if you prefer calculated their SUM).
The PLACE VALUE thing has never gone away and it is important for you to realize that even with a calculator - you are adding (taking the SUM) of each PLACE VALUE. All of the ONES are added together, then all of the TENS are added together, then the HUNDREDS and so on . .
I don't mean to insult your intelligence - but you really need to be sure that you are careful when drinking your Dr. Pepper or Tab so that you do not MIX UP the place value positions when you add (calculate a SUM) to determine a total value. Just like Coke and Root Beer do not mix well together, mixing place values will give you something entirely different than what you were expecting.
F
Whole Number Summary
After completing this lesson you should have mastered the following concepts:
1) Finding the PLACE VALUE of a DIGIT in a WHOLE NUMBER.
Determine the place value of the digit 5 in each whole number.
1. 657 2. 905 3. 5423 4. 6527 5. 43,526,000 6. 79,050,000 7. 5,408,092 8. 51,682,700
answers:
1) tens 2) ones 3) thousands 4) hundreds 5) hundred-thousands 6) ten-thousands 7) millions
8) ten-millions
Do you remember the meaning of the terms a) place value, b) digit and c) whole number?
2) Writing a WHOLE NUMBER in words and in STANDARD FORM.
Write each whole number in words.
9) 354 10) 316 11) 8279 12) 5445 13) 26,990 14) 42,009 15) 2,388,000 16) 3,204,000 17) 24,350,185 18) 47,033,107
answers:
9) three hundred fifty four 10) three hundred sixteen 11) eight thousand, two hundred seventy-nine 12) five thousand, four hundred forty-five 13) twenty-six thousand, nine hundred ninety 14) forty-two thousand, nine 15) two million, three hundred eighty-eight thousand 16) three million, two hundred four thousand 17) twenty-four million, three hundred fifty thousand, one hundred eighty-five 18) forty-seven million, thirty-three thousand, one hundred seven
To write a whole number in words and in standard from, write the number in each period followed by the name of that period.
To write a whole number in standard form, write the number in each period followed by a comma.
3) Write a WHOLE NUMBER in EXPANDED form.
Expanded form is a way to write numbers by showing the value of each digit.
Write each whole number in expanded form.
47) 406 48) 789 49) 3470 50) 6040
answers:
47) 400 + 6 48) 700 + 80 + 9 49) 3000 + 400 + 70 50) 6000 + 40
4) Read and understand the purpose of TABLES.
REMEMBER THAT THE PURPOSE OF A TABLE IS TO ORGANIZE DATA TO ALLOW EASY ANALYSIS OF THE NUMBERS.
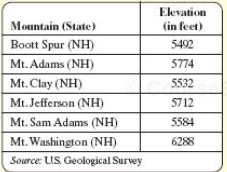The table shows the six tallest mountains in New England and their elevations. Use this table to answer the questions
1) Finding the PLACE VALUE of a DIGIT in a WHOLE NUMBER.
Determine the place value of the digit 5 in each whole number.
1. 657 2. 905 3. 5423 4. 6527 5. 43,526,000 6. 79,050,000 7. 5,408,092 8. 51,682,700
answers:
1) tens 2) ones 3) thousands 4) hundreds 5) hundred-thousands 6) ten-thousands 7) millions
8) ten-millions
Do you remember the meaning of the terms a) place value, b) digit and c) whole number?
| Digits are 0,1,2,3,4,5,6,7,8,9 which are used to write numbers. Place value is the POSITION of each DIGIT in a number. Whole numbers are defined as 0,1,2,3,4,5,6,7,8,9,10,11, . . . Natural numbers are whole numbers NOT COUNTING the number "0". For more problems like the ones listed below - follow this link . . .  1) What place is 3 in 40730 ? a. Ones b. Tens 2) What place is 4 in 6547 ? a. Ones b. Tens 3) What place is 7 in 896547 ? a. Ones b. Tens 4) What place is 1 in 3418 ? a. Ones b. Tens 5) What place is 1 in 14 ? a. Ones b. Tens 6) What place is 1 in 41 ? a. Ones b. Tens | |||||
| |||||
| |||||
| |||||
| |||||
| |||||
| 9) Which digit is in the ONES place? 91 | |||||
| 10) Which digit is in the TENS place? 94 | |||||
| The position of a digit (the place value of a number) determines the value of the number and indicates that the number has been written in STANDARD FORM (see link below). |
Write each whole number in words.
9) 354 10) 316 11) 8279 12) 5445 13) 26,990 14) 42,009 15) 2,388,000 16) 3,204,000 17) 24,350,185 18) 47,033,107
answers:
9) three hundred fifty four 10) three hundred sixteen 11) eight thousand, two hundred seventy-nine 12) five thousand, four hundred forty-five 13) twenty-six thousand, nine hundred ninety 14) forty-two thousand, nine 15) two million, three hundred eighty-eight thousand 16) three million, two hundred four thousand 17) twenty-four million, three hundred fifty thousand, one hundred eighty-five 18) forty-seven million, thirty-three thousand, one hundred seven
| 1) 1 x 10 + 8 x 1 = |
| 2) 4 x 10 + 6 x 1 = |
| 3) 1 x 10 = |
| 4) 8 x 10 = |
| 5) 1 x 10 + 2 x 1 = |
To write a whole number in words and in standard from, write the number in each period followed by the name of that period.To write a whole number in standard form, write the number in each period followed by a comma.
3) Write a WHOLE NUMBER in EXPANDED form.
Expanded form is a way to write numbers by showing the value of each digit.
Write each whole number in expanded form.
47) 406 48) 789 49) 3470 50) 6040
answers:
47) 400 + 6 48) 700 + 80 + 9 49) 3000 + 400 + 70 50) 6000 + 40
4) Read and understand the purpose of TABLES.
REMEMBER THAT THE PURPOSE OF A TABLE IS TO ORGANIZE DATA TO ALLOW EASY ANALYSIS OF THE NUMBERS.
The table shows the six tallest mountains in New England and their elevations. Use this table to answer the questions
1) Write the elevation of Mt. Clay in standard form and then in words. 5532; five thousand, five hundred thirty-two
2) Write the height of Boott Spur in expanded form. 5000 + 400 + 90 + 2
3) Write the height of Mt. Jefferson in expanded form. 5000 + 700 + 10 + 2
4) Which mountain is the tallest in New England? Mt. Washington
5) Write the elevation of Mt. Washington in standard form and then in words. 6288; six thousand, two hundred eighty-eight
6) Which mountain is the second tallest in New England? Mt Adams.
Using this list of words/terms fill in the blank of the following questions.
standard form, period, whole, expanded form, place value, words
1. The numbers 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, … are called __________ numbers.
2. The number 1,286 is written in __________ .
3. The number “ twenty- one” is written in ____________ .
4. The number 900 + 60 + 5 is written in _______________.
5. In a whole number, each group of three digits is called a( n) _____________ .
6. The ____________ of the digit 4 in the whole number 264 is ones.
dldld
Wednesday, April 29, 2015
Reading Tables
There are different ways that numbers can be presented and/or organized. One of these ways is to organize WHOLE NUMBERS in a table.
In the image below we see WHOLE numbers that have been placed on a table (LOL).
 |
| Whole Numbers ON A table |
For example the TABLE shown below has organized the ice cream cone sales by day and also by flavor.
The reason for this type of ORGANIZATION is so that the whole numbers can be ANALYZED to determine things like . . . which flavor sales better . . . which day are the most cones sold . . .
Using this type of ANALYSIS the ice cream person can decide to reduce his inventory and no longer offer the LEAST popular item such as THE CRUNCH BAR.
Another determination can also be made regarding sales on a particular day . . . After ANALYZING the data on this table it can be determined that sales on Monday total 316 cones, sales on Tuesday total 213 cones and sales on Wednesday total 327 cones.
Using this data the ice cream seller can choose to close his stand on the least popular day and hire extra help on the busiest days.
In the table shown below you will notice how whole numbers are used to organize the amount of ice cream cones that were sold by flavor and day.
Obviously - numbers can be organized to represent an endless number of facts about an endless list of topics.
Use this table to answer the following questions.
1) How many Sundae Cones were sold on Tuesday?
2) How many Crunch Bars were sold on Wednesday?
3) What was the total number of ice creams sold on Wednesday?
4) How many more Chocolate Éclair Bars were sold on Wednesday than on Monday?
5) What was the total number of Crunch Bars sold on the 3 days?
6) What was the total number of ice creams sold on Monday?
7) On which day were the most Sundae Cones sold?
8) On which day were the least Crunch Bars sold?
9) How many more Strawberry Shortcakes were sold on Monday than on Wednesday?
10) What was the total number of Ice Cream Sandwiches sold on the 3 days?
Now that we understand about place value and how to read and write whole numbers we will move to the next step which is a way to ORGANIZE these whole numbers so that we can ANALYZE what these numbers are showing us.
Tables like the one shown below are often used to ORGANIZE and display facts that involve numbers. If you will recall the ice cream table above, you can see how the numbers were organized so that we could easily analyze them to determine the most popular flavor etc) . . .
Analyze the table below to SEE what the numbers are showing us as indicated in this example . . . by reading from left to right along the row marked “ United States,” we find that the United States has 68 Chemistry, 54 Economics, 11 Literature, 22 Peace, 90 Physics, and 97 Physiology and Medicine Nobel Prize winners.
Use the table below to ANALYZE the data given and answer questions 1 through 4.
1) How many total Nobel Prize winners are from Sweden?
2) Which countries shown have fewer Nobel Prize winners than Russia?
3) How many Nobel Prize winners in Literature come from France?
4) Which countries shown have more than 60 Nobel Prize winners?
Solution to "table" questions:
1) Find “ Sweden” in the left column. Then read from left to right until the “ Total” column is reached. We find that Sweden has 32 Nobel Prize winners.
2) Russia has 20 Nobel Prize winners. Japan has 17, Netherlands has 16, and Italy has 15, so they have fewer Nobel Prize winners than Russia.
3) 15
4) United States, United Kingdom, and Germany.
Answers
1. 23
2. 17
3. 327
4. 59
5. 48
6. 316
7. Monday
8. Tuesday
9. 9
10. 856
ZZZ
Wtriting in Standard Form
 |
| Figure A |
By STANDARD FORM we are referring to how the digits are separated into groups by commas.
Starting from the right each group of three digits are separated into groups of three. Each group of
three digits is called a PERIOD. The names of the first four PERIODS are shown in (figure A)
Writing a WHOLE NUMBER in words: To write a WHOLE NUMBER in words, write the number in each PERIOD followed by the name of the PERIOD. "The ONES PERIOD is usually not written". The same procedure can be used when we read a WHOLE NUMBER.
Example: 245,978
The position occupied by the "2" is the hundred-thousands (see the 6 in the figure A). Putting a "2" in this position means that there are 2 hundred-thousands or TWO HUNDRED thousand.
Using the same procedure, putting a "4" in the ten-thousands position means that there are "4" ten-thousands for FORTY thousands because 4 tens ( 4x10) is forty.
Finally we put the five in the thousands position and this means that there are 5 thousands or FIVE thousand.
Notice how we read the number. "2" (using the periods chart above) the "2" is read as TWO (from the position on the chart the "2" is positioned in the period labeled) HUNDRED-THOUSAND so we say TWO HUNDRED THOUSAND . . . "4" (from the chart we see that the "4" is positioned in the period labeled) TEN THOUSAND -- since 4 x 10 = 40 we SAY forty thousand . . . "5" (from the chart we see that the 5 is positioned in the period labeled) THOUSAND so we say FIVE THOUSAND.
Tuesday, April 28, 2015
Place value
Digits 0,1,2,3,4,5,6,7,8, and 9 can be used to write numbers.
Examples of WHOLE numbers are made up of digits, and are as follows: 0,1,2,3,4,5,6,7,8,9,10,11,12,13,14, . . .
There is another type of number which is made up of WHOLE numbers. These numbers are called NATURAL numbers.
------- The smallest digit is "0".
------- The largest digit is (there is no largest digit) because the series of dots ". . . " means that the list
-------- goes on and on forever without ending.
++++ The smallest NATURAL number is "1" while the smallest WHOLE number is "0".
++++ The largest NATURAL number is (there is no largest) remember the ". . ." thing?
 |
| Figure A |
zzThe significance of the (figure A) is that whole numbers are used in mathematical operations.
A whole number is made up of digits (see list above).
====== Mathematical operations are things that we DO to numbers like addition, subtraction,
====== multiplication and so on. These operations always follow established rules so that
====== when you add 1 + 1 and get 2, this is the same answer that everyone else will get when
====== they add 1 + 1.
PLACE VALUE
 |
| LINK TO INTERACTIVE LESSON |
These digits are all whole numbers. You will notice however that there are two "3s" in this value. Even though the number "3" is repeated, they DO NOT represent the SAME value.
The reason for this is because that each one of the "3s" are placed in a different POSITION .
The PLACE value of the 3 on the left is HUNDRED THOUSANDS while the value of the 3 on the right is TEN-THOUSANDS.
Notice how THE PLACE of each digit is what actually determines its VALUE. This is why we have the term PLACE VALUE.
The digit whether it is 0 or 9 is the first step in determining the value - however the final step in determining the VALUE is where you put the digit.
####### Think of it like this; if there is a dollar bill on the table it is worth a dollar, but it has little
####### value to YOU because it is on the table.
####### If the dollar is in YOUR hand it has a certain value to YOU, if it is in your neighbors hand
####### the dollar is still worth 100 pennies, but it now has little VALUE to you.
####### In this simple example, nothing about the dollar bill changed except its LOCATION.
####### Likewise a digit can stay the same and only change LOCATION in the PLACE VALUE
####### chart meaning that its value is dependent upon its LOCATION just like the value of money
####### is dependent upon whether it is in your hands or your neighbors hand.
Sample problem:
Find the PLACE VALUE of the digit 7 in each whole number listed below:
*****1) 37,860,004 ------- millions place
*****2) 68,790 -------- hundreds place
*****3) 478,936 --------- ten-thousands place
Consider the following number: Say this number out loud. When you do, notice how you pronounce the PLACE value of each digit.
3,256 ----- three THOUSAND, two HUNDRED and FIFTY SIX.
------- the three is in the thousands place, the two is in the hundreds place, the five is in the tens place and the six is in the ones place.
Sample problems:
1) For the number 2768, what does the 2 mean?
A 2 Units
B 2 Tens
![[image]](http://www.mathopolis.com/questions/images/d/9/baf23d711ae7e9b4f852933ae852102.gif)
C 2 Hundreds
D 2 Thousands
Then the 2 means 2 Thousands
2) For the number 9053, what does the 0 mean?
A 0 Units
B 0 Tens
C 0 Hundreds
D 0 Thousands
![[image]](https://lh3.googleusercontent.com/blogger_img_proxy/AEn0k_vaqawghyi_OgpibS5xYHKOIgJcbhJIPRXgLw1UNTQy_wBL6bnKqNg9yFLg-qZHeOzw8qoMGt1mBjaKtzAsIQOmmnMSfPd5lXPskWzqBEeMUDm8PxNYLbxq5Ctk8hdCPHGhcIJjkAeN2PV3fcY0AExCVMjSqGc=s0-d)
Therefore the 0 means 0 Hundreds.
![[image]](http://www.mathopolis.com/questions/images/9/b/0be84ce0bcb89b0230c8200c9df2922.gif)
Therefore the 0 means 0 Hundreds.
Subscribe to:
Posts (Atom)