Perimeter of a polygon

Perimeter of Polygons:  Before we address this topic we need to define the two terms Perimeter and Polygon:  The perimeter is the distance around the outside edge of a shape.  A polygon is simply a shape as described below.

A POLYGON is a closed TWO DIMENSIONAL figure bounded by three OR MORE line segments.

You will notice that the BLUE figures are all polygons.  They are flat (two dimensional figures) that are CLOSED (the black line segments completely enclose the blue interior).

There are THREE things that prevent the PINK figures from being considered POLYGONS

1) they are not flat (they are three dimensional)
2) they are made up of CURVED segments
3) they are not completely enclosed.

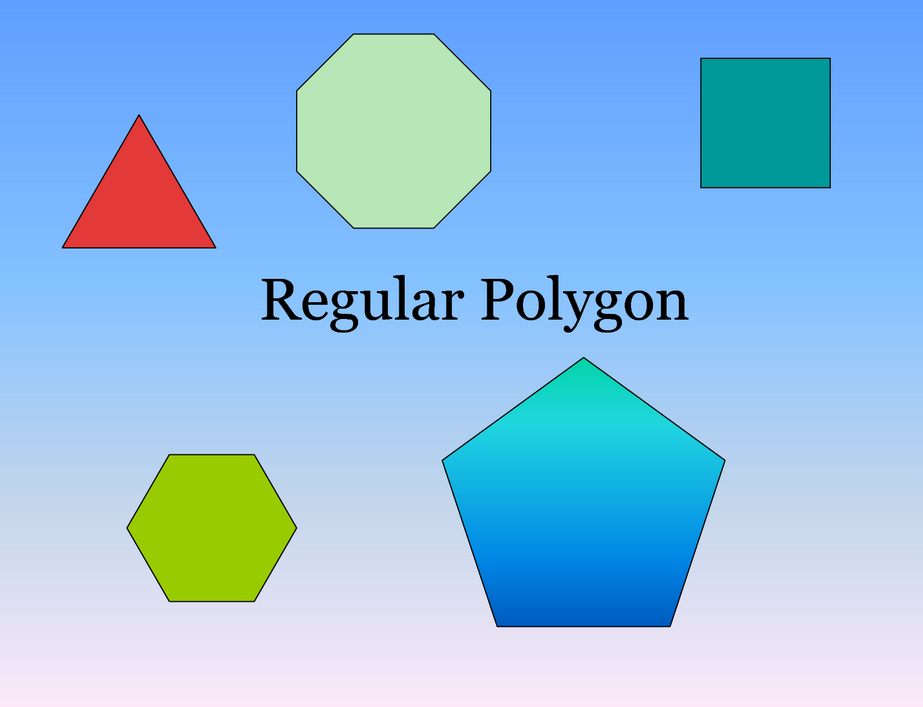There are TWO different kinds or types of polygons - they are named REGULAR POLYGONS and IRREGULAR POLYGONS . . .

 As you can see by these two illustrations . . . the regular POLYGONS are what we refer to as STANDARD shapes, while the irregular polygon is a NOT NORMAL shapel

So any flat (two dimensional shape) that has NO CURVES - and is completely enclosed by at least THREE line segments is a POLYGON.

Now that we have defined a POLYGON - lets take a closer look at what is meant by a perimeter.

I chose to illustrate the concept of PERIMETER by using an image of a fence.  A fence like the one shown to the left is often used enclose a yard. 

In the other figure below - the entire "perimeter" of the property is shown by the fence that goes ALL THE WAY around the buildings (OK use your imagination) and pretend there is "a gate" to close the gap that you see making this figure an IRREGULAR POLYGON.

So have you been able to guess what a lesson on finding the perimeter of a polygon is going to be about?

If you were the owner of a fence building company, this lesson would be VERY important to you.  Your income would depend on how many feet of fence you were able to build for your customers.

OK here comes the boring technical stuff - but this stuff is what those who buy or sell fencing supplies to fence their property - use everyday . . .

A discussion about perimeters and polygons cannot begin without starting with the word GEOMETRY . . . is a word which refers to the use of math to analyze the properties of lines, angles and shapes.  This is not a textbook definition, but it will do for now.

In GEOMETRY we use the mathematical property of ADDITION to find or to calculate the perimeter of a polygon (how many feet of fencing material is required to enclose a yard/field).

Technically speaking the perimeter is the distance around the outer edge of the polygon.  This means that the perimeter of a polygon is the SUM of the lengths of its sides

In order to solve this problem all we need to do is to add up the lengths of all the sides.
2 in + 3 in + 1 in + 3 in + 4 in = 13 in

If we were to use our imaginations again and pretend that these units were given to us in feet as opposed to inches, we could determine how much fencing material would be required to enclose a yard with these dimensions.

Suppose you own a fence building company "Fred's Fencing".  Your rent is due at the end of the month and you have an opportunity to build this fence and earn enough to pay your rent.

If your rent is $750 a month and if fencing materials cost $10 per foot, what is the total dollar amount will you need to charge to make enough money on this job to pay this months rent?


First of all you will need  to FIND THE PERIMETER of this POLYGON (yard).

Add the sum of the line segments shown - 2 feet + 3 feet + 1 foot + 3 feet + 4 feet = 13 feet.

In the first place this would obviously not be a big enough yard to make very much money, especially not the $750 that we need to pay our rent.  But for the sake of illustration let's continue . . . 

Our fence is only 13 feet long: If our supplies cost $10 per foot, our total cost for materials will be $10 x 13 feet = $130.  If we need to CLEAR $750 above the cost of material, we will need to charge the customer the following"  $130 material cost + $750 labor = $ 880 for a thirteen foot section of a privacy fence.

Do you think this price is reasonable?

Just to be on the safe side - let's review addition the OLD FASHION way before calculators.  I KNOW that you have a calculator and that is a good thing, BUT it is really a good thing in mathematics when the "mathematician" (that is you) is smarter than the tools they use.

We have already used the term SUM.  So by now we should realize that a long time ago someone was not satisfied that there was already a perfectly good word called ADDITION.  This old word means just exactly what the new word SUM means and  that is "adding numbers together" to get a bigger number than we started with.

Why invent new words that mean the same thing as old words . . . I can remember when there were only a few flavors of soft drinks that had been invented and diet sodas did not even exist . . . All soft drinks quench our thirst - so why are there so many that do exactly the same thing?

If you prefer to use the word ADDITION that is OK . . . or if you choose to use the work SUM that will be OK too, because they both do and mean the same thing.  Do you prefer Coke, Sprite or Dr Pepper?

In previous lessons we discussed the terms DIGITS, WHOLE NUMBERS and PLACE VALUES . . . In this lesson we have added PERIMETER and POLYGON.

Notice the extra words that have been added to our vocabulary - "addend" why don't we use digit or whole number?  

Why do we prefer Pepsi over a Coke?  Study the illustration given above and notice how the PLACE VALUES are still present.  BEFORE calculators numbers were added together in columns just like the one shown.

The big problem in the OLDEN days was teaching the students to LINE THE NUMBERS properly when they added them together (or if you prefer calculated their SUM).

The PLACE VALUE thing has never gone away and it is important for you to realize that even with a calculator - you are adding (taking the SUM) of each PLACE VALUE.  All of the ONES are added together, then all of the TENS are added together, then the HUNDREDS and so on . .

I don't mean to insult your intelligence - but you really need to be sure that you are careful when drinking your Dr. Pepper or Tab so that you do not MIX UP the place value positions when you add (calculate a SUM) to determine a total value.  Just like Coke and Root Beer do not mix well together, mixing place values will give you something entirely different than what you were expecting.




 F

Whole Number Summary

After completing this lesson you should have mastered the following concepts:

1) Finding the PLACE VALUE of a DIGIT in a WHOLE NUMBER.

Determine the place value of the digit 5 in each whole number.
1. 657      2. 905     3. 5423     4. 6527      5. 43,526,000       6. 79,050,000     7. 5,408,092                   8. 51,682,700

answers:
1) tens 2) ones  3) thousands  4) hundreds  5) hundred-thousands  6) ten-thousands  7)  millions  
8) ten-millions


Do you remember the meaning of the terms a) place value, b) digit and c) whole number?

Digits are 0,1,2,3,4,5,6,7,8,9 which are used to write numbers.   Place value is the POSITION of each DIGIT in a number.   Whole numbers are defined as 0,1,2,3,4,5,6,7,8,9,10,11, . . . Natural numbers are whole          numbers NOT COUNTING the number "0". For more problems like the ones listed below - follow this link . . .  1)  What place is 3 in 40730 ?   a. Ones   b. Tens      2)  What place is 4 in 6547 ?  a. Ones   b. Tens    3)  What place is 7 in 896547 ?  a. Ones   b. Tens    4)  What place is 1 in 3418 ?  a. Ones   b. Tens    5)  What place is 1 in 14 ?  a. Ones   b. Tens     6)  What place is 1 in 41 ?  a. Ones   b. Tens

7)  What place is 1 in 14 ?  a. Ones   b. Tens     8)  what place is 4 in 74 ?  a. Ones   b. Tens 9)  What place is 4 in 41 ?  a. Ones   b. Tens    10)  What place is 9 in 69 ?  a. Ones   b. Tens     1)  Which digit is in the ONES place? 42  2)  Which digit is in the HUNDREDS place? 361

3)  Which digit is in the THOUSANDS place? 24683  4)  Which digit is in the TENS place? 398

5)  Which digit is in the HUNDREDS place? 786   6)  Which digit is in the TENS place? 379

7)  Which digit is in the ONES place? 87

8)  Which digit is in the THOUSANDS place? 86517

9)  Which digit is in the ONES place? 91

10)  Which digit is in the TENS place? 94

The position of a digit (the place value of a number) determines the value of the number and indicates that the number has been written in STANDARD FORM (see link below).

2) Writing a WHOLE NUMBER in words and in STANDARD FORM.

Write each whole number in words.
9) 354    10) 316    11) 8279    12) 5445    13) 26,990    14) 42,009    15) 2,388,000    16) 3,204,000 17)  24,350,185    18) 47,033,107

answers:
9) three hundred fifty four   10) three hundred sixteen  11)  eight thousand, two hundred seventy-nine  12) five thousand, four hundred forty-five 13) twenty-six thousand, nine hundred ninety  14)  forty-two thousand, nine   15)  two million, three hundred eighty-eight thousand 16)  three million, two hundred four thousand 17)  twenty-four million, three hundred fifty thousand, one hundred eighty-five  18)  forty-seven million, thirty-three thousand, one hundred seven

1)  1 x 10 + 8 x 1 =

2)  4 x 10 + 6 x 1 =

3)  1 x 10 =

4)  8 x 10 =

5)  1 x 10 + 2 x 1 =

To write a whole number in words and in standard from, write the number in each period followed by the name of that period.

To write a whole number in standard form, write the number in each period followed by a comma.


3) Write a WHOLE NUMBER in EXPANDED form.
Expanded form is a way to write numbers by showing the value of each digit.

 Write each whole number in expanded form.
 47) 406    48) 789    49) 3470    50) 6040

 answers:
47)  400 + 6    48)  700 + 80 + 9     49)  3000 + 400 + 70   50)  6000 + 40

4) Read and understand the purpose of TABLES.

REMEMBER THAT THE PURPOSE OF A TABLE IS TO ORGANIZE DATA TO ALLOW EASY ANALYSIS OF THE NUMBERS.

The table shows the six tallest mountains in New England and their elevations. Use this table to answer the questions  

1)  Write the elevation of Mt. Clay in standard form and then in words.  5532; five thousand, five hundred thirty-two

2)  Write the height of Boott Spur in expanded form. 5000 + 400 + 90 + 2

3)  Write the height of Mt. Jefferson in expanded form.  5000 + 700 + 10 + 2

4)  Which mountain is the tallest in New England?  Mt. Washington

5)  Write the elevation of Mt. Washington in standard form and then in words. 6288; six thousand, two hundred eighty-eight

6)   Which mountain is the second tallest in New England?  Mt Adams.

Using this list of words/terms fill in the blank of the following questions.

standard form,  period,  whole,  expanded form,  place value,  words

1. The numbers 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, … are called __________ numbers. 

2. The number 1,286 is written in __________ .

3. The number “ twenty- one” is written in ____________ . 

4. The number 900 + 60 + 5 is written in _______________. 

5. In a whole number, each group of three digits is called a( n) _____________ . 

6. The ____________ of the digit 4 in the whole number 264 is ones.

dldld

Reading Tables

There are different ways that numbers can be presented and/or organized.  One of these ways is to organize WHOLE NUMBERS in a table.  

 In the image below we see WHOLE numbers that have been placed on a table (LOL).

Whole Numbers ON A table

The purpose of a math TABLE is to organize numbers relative to different types of criteria.  

For example the TABLE shown below has organized the ice cream cone sales by day and also by flavor.

The reason for this type of ORGANIZATION is so that the whole numbers can be ANALYZED to determine things like . . . which flavor sales better . . . which day are the most cones sold . . . 

Using this type of ANALYSIS  the ice cream person can decide to reduce his inventory and no longer offer the LEAST popular item such as THE CRUNCH BAR.

Another determination can also be made regarding sales on a particular day . . . After ANALYZING the data on this table it can be determined that sales on Monday total 316 cones, sales on Tuesday total 213 cones and sales on Wednesday total 327 cones.

Using this data the ice cream seller can choose to close his stand on the least popular day and hire extra help on the busiest days.

In the table shown below you will notice how whole numbers are used to organize the amount of ice cream cones that were sold by flavor and day.

Obviously - numbers can be organized to represent an endless number of facts about an endless list of topics.

Use this table to answer the following questions.


1)  How many Sundae Cones were sold on Tuesday? 
2) How many Crunch Bars were sold on Wednesday?
3) What was the total number of ice creams sold on Wednesday?
4) How many more Chocolate Éclair Bars were sold on Wednesday than on Monday?
5) What was the total number of Crunch Bars sold on the 3 days?
6) What was the total number of ice creams sold on Monday?
7) On which day were the most Sundae Cones sold?
8) On which day were the least Crunch Bars sold? 
9) How many more Strawberry Shortcakes were sold on Monday than on Wednesday?
10)  What was the total number of Ice Cream Sandwiches sold on the 3 days?

Now that we understand about place value and how to read and write whole numbers we will move to the next step which is a way to ORGANIZE these whole numbers so that we can ANALYZE what these numbers are showing us.

Tables like the one shown below are often used to ORGANIZE and display facts that involve numbers.  If you will recall the ice cream table above, you can see how the numbers were organized so that we could easily analyze them to determine the most popular flavor etc) . . .

Analyze the table below to SEE what the numbers are showing us as indicated in this example . . . by reading from left to right along the row marked “ United States,” we find that the United States has 68 Chemistry, 54 Economics, 11 Literature, 22 Peace, 90 Physics, and 97 Physiology and Medicine Nobel Prize winners.

Use the table below to ANALYZE the data given and answer questions 1 through 4.

1) How many total Nobel Prize winners are from Sweden? 
2) Which countries shown have fewer Nobel Prize winners than Russia?
3) How many Nobel Prize winners in Literature come from France? 
4) Which countries shown have more than 60 Nobel Prize winners?

Solution to "table" questions:
1) Find “ Sweden” in the left column. Then read from left to right until the “ Total” column is reached. We find that Sweden has 32 Nobel Prize winners.
2) Russia has 20 Nobel Prize winners. Japan has 17, Netherlands has 16, and Italy has 15, so they have fewer Nobel Prize winners than Russia.
3) 15
4) United States, United Kingdom, and Germany.











Answers

1. 23

2. 17

3. 327

4. 59

5. 48

6. 316

7. Monday

8. Tuesday

9. 9

10. 856

ZZZ

Wtriting in Standard Form

Figure A

 A whole number such as 1,083,664,500 is written in what we refer to as STANDARD FORM.

By STANDARD FORM we are referring to how the digits are separated into groups by commas.

Starting from the right each group of three digits are separated into groups of three.  Each group of

three digits is called a PERIOD.  The names of the first four PERIODS are shown in (figure A)

Writing a WHOLE NUMBER in words:  To write a WHOLE NUMBER in words, write the number in each PERIOD  followed by the name of the PERIOD.  "The ONES PERIOD is usually not written".  The same procedure can be used when we read a WHOLE NUMBER.

Example:  245,978

The position occupied by the "2" is the hundred-thousands (see the 6 in the figure A).  Putting a "2" in this position means that there are 2 hundred-thousands or TWO HUNDRED thousand.

Using the same procedure, putting a "4" in the ten-thousands position means that there are "4" ten-thousands for FORTY thousands because 4 tens ( 4x10) is forty.

Finally we put the five in the thousands position and this means that there are 5 thousands or FIVE thousand.

Notice how we read the number.  "2" (using the periods chart above) the "2" is read as TWO (from the position on the chart the "2" is positioned in the period labeled) HUNDRED-THOUSAND so we say TWO HUNDRED THOUSAND  . . . "4" (from the chart we see that the "4" is positioned in the period labeled) TEN THOUSAND -- since 4 x 10 = 40 we SAY forty thousand . . . "5" (from the chart we see that the 5 is positioned in the period labeled) THOUSAND so we say FIVE THOUSAND.

Place value

Digits 0,1,2,3,4,5,6,7,8, and 9 can be used to write numbers.

Examples of WHOLE numbers are made up of digits, and are as follows: 0,1,2,3,4,5,6,7,8,9,10,11,12,13,14, . . .

There is another type of number which is made up of WHOLE numbers.  These numbers are called NATURAL numbers.

------- The smallest digit is "0".
------- The largest digit is (there is no largest digit) because the series of dots ". . . " means that the list
-------- goes on and on forever without ending.

++++ The smallest NATURAL number is "1" while the smallest WHOLE number is "0".
++++ The largest NATURAL number is (there is no largest) remember the ". . ." thing?

Figure A

zzThe significance of the (figure A) is that whole numbers are used in mathematical operations.

A whole number is made up of digits (see list above).

====== Mathematical operations are things that we DO to numbers like addition, subtraction,
====== multiplication and so on.  These operations always follow established rules so that
====== when you add 1 + 1 and get 2, this is the same answer that everyone else will get when
====== they add 1 + 1.

PLACE VALUE

LINK TO INTERACTIVE LESSON

In the image to the right you will notice the distance between Mercury and Earth is given using the following digits:  48,337,000

These digits are all whole numbers.  You will notice however that there are two "3s" in this value.  Even though the number "3" is repeated, they DO NOT represent the SAME value.

The reason for this is because that each one of the "3s" are placed in a different POSITION  .

The PLACE value of the 3 on the left is HUNDRED THOUSANDS while the value of the 3 on the right is TEN-THOUSANDS.

Notice how THE PLACE of each digit is what actually determines its VALUE.  This is why we have the term PLACE VALUE.

The digit whether it is 0 or 9 is the first step in determining the value - however the final step in determining the VALUE is where you put the digit.

####### Think of it like this; if there is a dollar bill on the table it is worth a dollar, but it has little
####### value to YOU because it is on the table.

####### If the dollar is in YOUR hand it has a certain value to YOU, if it is in your neighbors hand
####### the dollar is still worth 100 pennies, but it now has little VALUE to you.

####### In this simple example, nothing about the dollar bill changed except its LOCATION.
####### Likewise a digit can stay the same and only change LOCATION in the PLACE VALUE
####### chart meaning that its value is dependent upon its LOCATION just like the value of money
####### is dependent upon whether it is in your hands or your neighbors hand.

Sample problem:

Find the PLACE VALUE of the digit 7 in each whole number listed below:
*****1) 37,860,004   ------- millions place
*****2) 68,790   -------- hundreds place
*****3) 478,936  --------- ten-thousands place

Consider the following number:  Say this number out loud.  When you do, notice how you pronounce the PLACE value of each digit.

3,256 ----- three THOUSAND, two HUNDRED and FIFTY SIX.

------- the three is in the thousands place, the two is in the hundreds place, the five is in the tens place and the six is in the ones place.

Sample problems:

1)  For the number 2768, what does the 2 mean?

A    2 Units                    

B    2 Tens

C    2 Hundreds

D    2 Thousands

Then the 2 means 2 Thousands







2) For the number 9053, what does the 0 mean?

A   0 Units

B   0 Tens

C   0 Hundreds

D   0 Thousands

                                                      Therefore the 0 means 0 Hundreds.

Pythagorean Theorem

/2 Pythagorean Theorem

The Pythagorean Theorem Figure (1)

One important application of square roots has to do with right triangles.  Do your remember what a right triangle is.  The RIGHT TRIANGLE is a triangle where one of the angles is a RIGHT ANGLE or one that measures 90 degrees.

The hypotenuse of the right triangle is the side that is opposite of the right angle.  The right angle 

Fig (2)

is symbolized by the image "Figure (2).



In the figure (1) above, side "c" is opposite the "right angle" that is shown in the "right triangle".

               CLICK FIG (3) FOR VIDEO

Figure (3)

When a triangle has a right angle (90°) . . . and if the squares are made on each of the three sides as shown . . . then the biggest square (the red one) has the EXACT SAME AREA as the "SUM" of the other two.

What this means is that if we find the area of the green square "a" and add this to the area of the purple square "b" then the result will be the area of the red square "c".

So figure (3) is a visual definition (representation) of the Pythagorean Theorem . . . while the following is the non-visual representation of the same thing.

     CLICK FIG (4) TO VIEW

Example of AREA fig (4)

a² + b² = c²  . . . In previous lessons we learned about finding the area of squares.  The reason that these lessons PRECEDED this current lesson on the Pythagorean Theorem is because when we use the Pythagorean Theorem we are actually finding the area of the missing squares shown in figure (3).

The AREA of any shape is simply "the size" of the surface.  In fig (4) you will notice that the AREA of each shape is 9 square units.

Notice the square shape in this figure, it can be described for us as having three blocks in the horizontal direction (sideways/back and forth) {1,2,3}.  It can also be described for us as having three blocks in the vertical direction (up and down) {1,4,7}.

The AREA or the SIZE of this square is determined by simply counting the squares that are contained inside the square.  When we do this, we count a total of NINE squares and we write this down as 9 square inches, or 9 square cm . . .

In this particular instance we counted NINE squares within the square.  We can also use MULTIPLICATION to do the same thing.  Supposing the square were much larger (for instance the outside wall of a block building), rather than counting each individual block that is used in the wall, we could could count the blocks along the lower edge and also the number of blocks along ONE outside edge as shown to us in figure (5).

Figure (5)

Use your imagination here, the number 3 along the left side of the image can represent 3 blocks, 3 feet, 30 feet or 300 feet.  The same is true of the number 5 along the top, it could represent 5 block, 5 feet, 50 feet or 500 feet - you get the idea.

The FORMULA for finding the area {the size} of a FLAT surface is always the same.  Either each individual block or square on the shape is counted OR the length of one side is multiplied by the length of a perpendicular side as shown.

Now that we have reviewed the concept of AREA, lets recall our knowledge of SQUARE ROOTS.

At this point in our lesson - when we mention SQUARE ROOTS, we should not be introducing an unfamiliar concept.  In the figure (5) above, the square unit area of the rectangle is 3 x 5 or 15 square units.  Conversely if we work BACKWARDS from a given surface area, how do we find the respective SIDES of the shape that resulted in our 15 square unit size?

I wanted to use this 3 x 5 rectangle to illustrate the point that when we mention the Pythagorean Theorem, we are only talking about SQUARES not rectangles.

If we take the SQUARE ROOT of 15, the answer is ≈ 3.87.  What this means is that a SQUARE with each of it's four sides measuring ≈ 3.87 will produce an AREA of 15 square units of measure.  

You will note however that the shape in figure (5) is NOT a square and the sides shown are NOT ≈ 3.87 each but rather 3 and 5 respectively . . . consequently the PYTHAGOREAN THEOREM does not apply to any shape other than a SQUARE.

Figure (6)

Notice figure (6).  See how we get the term "3 squared"?  In this instance 3 square units x 3 square units = 9 square units.

We could also say 3² = 9.  Now if we started with 9 square units that represented the SIZE of the square in figure (6) and wanted to work 

BACKWARDS to determine the length of the width and the height of the square, we would change directions and simply use the concept of SQUARE ROOTS.

CLICK IMAGE FOR VIDEO LESSON ON SQUARE ROOTS

NOW our knowledge of ALGEBRA comes in handy here.  By this I refer to how we can solve for the missing value in the equation given as a² + b² = c².

If we know the value of any two of these three variables, then using ALGEBRA we can "solve" for the third variable that is missing.

Fig (7)

But before we begin to use our knowledge of ALGEBRA to solve for the missing variable (the side of one of the RIGHT triangles), we will have a brief review of "how to find X" in a standard ALGEBRAIC equation because this will be exactly what we will be doing with the Pythagorean Theorem.

Think about the word ALGEBRA as really being a PUZZLE . . . for instance: if we have two apples how many more apples do we need before we have a total of four?  Algebra really is that simple!

Fig (7)

 ____ + 2 = 4  We usually see this type of equation written as follows with the instruction given as FIND X in the equation:

X + 2 = 4 which actually means . . . if we have a total of 4 apples, how many more apples must ADD to the two that we already have to make the equation true?

Another example might be like this:  One apple added to another apple results in a total of 2 apples.  In equation form this would be written as 

We may already know that we have a total of two apples.  We might then be asked, "If one apple weights 1/2 pound, how much will two apples weight?

fig (8)

The solution is found using ALGEBRA . . . if one apple weights 1/2 pound and if you have two apples . . . then the solution is found by substituting 1/2 pound for each apple symbol in figure (8).

!/2 lb + 1/2 lb = 1 lb . . . ALGEBRA is all about changing, interchanging and in some cases INTERCHANGING SYMBOLS with numbers.  As we proceed in to higher levels of ALGEBRA, the problems do get a bit more complex but the concept remains as simple as described in this review.

Now we are ready for the Pythagorean Theorem!  Which uses the concept of AREA to solve for the unknown lengths of the sides of a RIGHT TRIANGLE.

Do you know what the term "hypotenuse" means?  In words the hypotenuse is the side of a triangle that is opposite of the right angle in a RIGHT ANGLED triangle.

Notice that all three sides of this triangle are named.  Notice the Greek symbol "θ" . . . this symbol represents an angle.  The idea is that the length of the side that is opposite the value of this angle is on one side of the 90° while the length of the side that is adjacent to the value of this angle is on the other side of the 90°.

Go back to the beginning of this lesson and review figure (3).  The three squares are all of different sizes.  The lengths of the four sides of the green square are all equal to one another.  The lengths of the four sides of the purple square are all equal to one another.  The lengths of the four sides of the red square are all equal to one another.

Figure (3)

Since the four SIDES of each one of the respective squares are equal to "each other" (but NOT equal to the lengths of the sides of the OTHER squares) . . . then one side of each square represents ONE LEG of the right triangle shown in fig (3).

a = to the length of all four sides of the green square.

b = to the length of all four sides of the purple square.

c = to the length of all four sides of the red square.

The calculated area of square a ADDED to the calculated area of square b is equal in value to the calculated area of square c.   This is what a² + b² = c² means.

Sample Questions: Only one of these triangles is really a right triangle.  Which one is it?

Sample problem (1)

Which of the following describes the triangle shown?





 

An isocseles right angled triangle

A scalene obtuse angled triangle

A scalene acute angled triangle

A scalene right angled triangle

FOLLOW THIS LINK FOR PRACTICE PROBLEMS